Polar equations: Difference between revisions
>Mindraker No edit summary |
>NecroBumpist <br>rrrrrr, it's cold in here. Reworked a bunch of the examples to have syntax highlighting (where there was <pre> or none). Replaced a few images. Fun stuff. |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
Roblox operates using the [http://en.wikipedia.org/wiki/Cartesian_coordinate_system Cartesian coordinate system]. This is a gridlike system much like the tiles on the floor of a bathroom. This system is ideal for certain things, e.g., straight lines, roads, buildings, tiles. It is not as good for other things, such as spirals. Another system, called the [http://en.wikipedia.org/wiki/Polar_coordinate_system Polar coordinate system] based on an angle and the distance from the center of a map, is much better suited for this. | |||
The problem with this is that you need to convert | == Introduction == | ||
The problem with this working in the Polar system is that you need to convert your results to the Cartesian system, because Roblox operates in it. This is actually easy enough to do, if you have a formula in the Polar system. Let's take the [http://en.wikipedia.org/wiki/Quadrifolium Quadrifolium] from Wikipedia. Its polar equation is: | |||
<!--Can someone rework this so all of these images fit in the Example box? Not a vertically, but next to each other at least.!--> | |||
[[Image:Polar1.PNG|thumb|{{`|=n, d = 2, 1}}(Quadrifolium)]] | |||
[[Image:Polar2.PNG|thumb|{{`|=n, d = 3, 2}}]] | |||
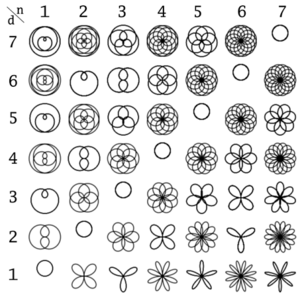
[[Image:Rhodonea curve.png|thumb|Rhodonea curves, with n and d listed.]] | |||
{{lua|= | |||
r = math.cos(2*theta) | |||
}} | |||
x | So, to obtain the values for x and z, we have to multiply r as follows: | ||
z | |||
{{lua|= | |||
x = r * math.cos(theta) | |||
z = r * math.sin(theta) | |||
}} | |||
We now get: | |||
{{lua|= | |||
x=math.cos(2*i) * math.cos(theta) | |||
z=math.cos(2*i) * math.sin(theta) | |||
}} | |||
You will see these formulas again in the script below. | |||
{{Example| | |||
{{lua|= | |||
local n=2 | |||
local d=1 | |||
local k = n/d | |||
for i = 1, 500, 1 do | |||
local x=math.cos(k*i) * math.cos(i) | |||
local z=math.cos(k*i) * math.sin(i) | |||
local p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z)) | |||
p.Size = Vector3.new(8,8,8) | |||
p.Anchored = true | |||
p.BottomSurface = "Smooth" | |||
p.TopSurface = "Smooth" | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | end | ||
}} | |||
}} | |||
Other curves can be set by changing the value of {{`|n}} and {{`|d}}, which in turn result in a change in {{`|k}}. | |||
== Archimedean spiral == | |||
This [http://en.wikipedia.org/wiki/Archimedean_spiral classic mathematical example] has a polar formula of: | |||
{{lua|= | |||
r = a + b*theta | |||
}} | |||
Similarly, using these conversion formulas, one arrives at the formulas used in the script further below: | |||
{{lua|= | |||
x = r*cos(theta) -- #1 | |||
y = r*sin(theta) -- #2 | |||
}} | |||
[[Image:Archimedes.PNG|thumb|Archimedean spiral]] | [[Image:Archimedes.PNG|thumb|Archimedean spiral]] | ||
{{lua|= | |||
local a = 1 | |||
local b = 1 | |||
for i = 1, 50, 0.1 do | |||
local x = (a+b*(i)) * math.cos(i) | |||
local z = (a+b*(i)) * math.sin(i) | |||
for i = 1,50, .1 do | |||
x=(a+b*(i)) * math.cos(i) | |||
z=(a+b*(i)) * math.sin(i | |||
local p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z)) | |||
p.Size = Vector3.new(8,8,8) | |||
p.Anchored = true | |||
p.BottomSurface = "Smooth" | |||
p.TopSurface = "Smooth" | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | end | ||
}} | |||
== 3-D images == | == 3-D images == | ||
Similarly, 3-D images can be created with a system similar to polar equations, called [http://en.wikipedia.org/wiki/Spherical_coordinate_system Spherical coordinates]. The formula for a sphere in polar is rho = R. Using the formula to convert Spherical coordinates to Cartesian: | Similarly, 3-D images can be created with a system similar to polar equations, called [http://en.wikipedia.org/wiki/Spherical_coordinate_system Spherical coordinates]. The formula for a sphere in polar is {{`|=rho = R}}. Using the formula to convert Spherical coordinates to Cartesian: | ||
x=r*sin(theta)*cos(phi) | {{lua|= | ||
y=r*sin(theta)*sin(phi) | x = r * math.sin(theta) * math.cos(phi) | ||
z=r*cos(theta) | y = r * math.sin(theta) * math.sin(phi) | ||
z = r * math.cos(theta) | |||
}} | |||
The formula rho = R is obvious below. | The formula {{`|=rho = R}} is obvious below. | ||
[[Image:Hollowspherepolar.PNG|thumb|Hollow sphere]] | [[Image:Hollowspherepolar.PNG|thumb|Hollow sphere]] | ||
{{lua|= | |||
local R=4 | |||
for i = 1,10, 1 do | for i = 1,10, 1 do | ||
for j = 1,10, .1 do | for j = 1,10, .1 do | ||
local x = R*math.sin(i)*math.cos(j) | |||
local y = R*math.sin(i)*math.sin(j) | |||
local z = R*math.cos(i) | |||
x=R*math.sin(i)*math.cos(j) | |||
y=R*math.sin(i)*math.sin(j) | |||
z=R*math.cos(i | |||
local p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z)) | |||
p.Size = Vector3.new(8,8,8) | |||
p.Anchored = true | |||
p.BottomSurface = "Smooth" | |||
p.TopSurface = "Smooth" | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | |||
end | end | ||
}} | |||
== Ellipsoids == | == Ellipsoids == | ||
Another example is the ellipsoid, very similar to the sphere above. Really all that's being changed are the radii (a, b, and c). | |||
Spherical formula: | |||
{{lua|= | |||
x = a*math.cos(theta)*math.sin(phi) | |||
y = b*math.sin(theta)*math.sin(phi) | |||
z = math.cos(phi) | |||
}} | |||
Conversion: | |||
x= | {{lua|= | ||
y= | x = r*math.sin(theta)*math.cos(phi) | ||
z=cos( | y = r*math.sin(theta)*math.sin(phi) | ||
z = r*math.cos(theta) | |||
}} | |||
Cartesian formula: | |||
x= | {{lua|= | ||
y= | x = a*math.sin(i)*math.cos(j) | ||
z= | y = b*math.sin(i)*math.sin(j) | ||
z = c*math.cos(i) | |||
}} | |||
[[Image:Hollowellipsoid.PNG|thumb|a=3, b=10, c=5]] | |||
{{Example| | |||
{{lua|= | |||
local a=3 -- radius | |||
local b=10 -- radius | |||
local c=5 -- radius | |||
a= | for i = 1, 50, 1 do | ||
for j = 1, 50, 1 do | |||
c | local x = a*math.sin(i)*math.cos(j) | ||
local y = b*math.sin(i)*math.sin(j) | |||
local z = c*math.cos(i) | |||
local p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(30*x, 30*y, 30*z)) | |||
p.Size = Vector3.new(8,8,8) | |||
p.Anchored = true | |||
p.BottomSurface = "Smooth" | |||
p.TopSurface = "Smooth" | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | |||
end | |||
}} | |||
}} | |||
By changing the values of {{`|a, b, and c}}, you can come up with [http://en.wikipedia.org/wiki/Ellipsoid different shapes]: | |||
<pre> | |||
a=b=c: Sphere | |||
a=b>c: Oblate spheroid (disk-shaped) | |||
a=b<c: Prolate spheroid (egg-shaped) | |||
a>b>c: Scalene ellipsoid ("three unequal sides") | |||
</pre> | </pre> | ||
== See also == | == See also == | ||
*[[Function_Dump/Mathematical_Functions|The Lua math library]] | |||
[http://en.wikipedia.org/wiki/Quadrifolium Wikipedia, Quadrifolium] | *[http://en.wikipedia.org/wiki/Quadrifolium Wikipedia, Quadrifolium] | ||
*[http://en.wikipedia.org/wiki/Rose_(mathematics) Rose curve] | |||
[http://en.wikipedia.org/wiki/Rose_(mathematics) Rose curve] | *[http://en.wikipedia.org/wiki/Polar_coordinate_system Polar coordinate system] | ||
*[http://en.wikipedia.org/wiki/Spherical_coordinate_system Spherical coordinate system] | |||
[http://en.wikipedia.org/wiki/Polar_coordinate_system Polar coordinate system] | |||
[http://en.wikipedia.org/wiki/Spherical_coordinate_system Spherical coordinate system] | |||
[[Category:Scripting Tutorials]] | [[Category:Scripting Tutorials]] | ||
Latest revision as of 00:43, 15 April 2012
Roblox operates using the Cartesian coordinate system. This is a gridlike system much like the tiles on the floor of a bathroom. This system is ideal for certain things, e.g., straight lines, roads, buildings, tiles. It is not as good for other things, such as spirals. Another system, called the Polar coordinate system based on an angle and the distance from the center of a map, is much better suited for this.
Introduction
The problem with this working in the Polar system is that you need to convert your results to the Cartesian system, because Roblox operates in it. This is actually easy enough to do, if you have a formula in the Polar system. Let's take the Quadrifolium from Wikipedia. Its polar equation is:


r = math.cos(2*theta)
So, to obtain the values for x and z, we have to multiply r as follows:
x = r * math.cos(theta)
z = r * math.sin(theta)
We now get:
x=math.cos(2*i) * math.cos(theta)
z=math.cos(2*i) * math.sin(theta)
You will see these formulas again in the script below.
local n=2
local d=1
local k = n/d
for i = 1, 500, 1 do
local x=math.cos(k*i) * math.cos(i)
local z=math.cos(k*i) * math.sin(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
Other curves can be set by changing the value of n and d, which in turn result in a change in k.
Archimedean spiral
This classic mathematical example has a polar formula of:
r = a + b*theta
Similarly, using these conversion formulas, one arrives at the formulas used in the script further below:
x = r*cos(theta) -- #1
y = r*sin(theta) -- #2

local a = 1
local b = 1
for i = 1, 50, 0.1 do
local x = (a+b*(i)) * math.cos(i)
local z = (a+b*(i)) * math.sin(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
3-D images
Similarly, 3-D images can be created with a system similar to polar equations, called Spherical coordinates. The formula for a sphere in polar is rho = R. Using the formula to convert Spherical coordinates to Cartesian:
x = r * math.sin(theta) * math.cos(phi)
y = r * math.sin(theta) * math.sin(phi)
z = r * math.cos(theta)
The formula rho = R is obvious below.

local R=4
for i = 1,10, 1 do
for j = 1,10, .1 do
local x = R*math.sin(i)*math.cos(j)
local y = R*math.sin(i)*math.sin(j)
local z = R*math.cos(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
end
Ellipsoids
Another example is the ellipsoid, very similar to the sphere above. Really all that's being changed are the radii (a, b, and c).
Spherical formula:
x = a*math.cos(theta)*math.sin(phi)
y = b*math.sin(theta)*math.sin(phi)
z = math.cos(phi)
Conversion:
x = r*math.sin(theta)*math.cos(phi)
y = r*math.sin(theta)*math.sin(phi)
z = r*math.cos(theta)
Cartesian formula:
x = a*math.sin(i)*math.cos(j)
y = b*math.sin(i)*math.sin(j)
z = c*math.cos(i)

local a=3 -- radius
local b=10 -- radius
local c=5 -- radius
for i = 1, 50, 1 do
for j = 1, 50, 1 do
local x = a*math.sin(i)*math.cos(j)
local y = b*math.sin(i)*math.sin(j)
local z = c*math.cos(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(30*x, 30*y, 30*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
end
By changing the values of a, b, and c, you can come up with different shapes:
a=b=c: Sphere
a=b>c: Oblate spheroid (disk-shaped)
a=b<c: Prolate spheroid (egg-shaped)
a>b>c: Scalene ellipsoid ("three unequal sides")