Polar equations
Roblox operates using the Cartesian coordinate system. This is a gridlike system much like the tiles on the floor of a bathroom. This system is ideal for certain things, e.g., straight lines, roads, buildings, tiles. It is not as good for other things, such as spirals. Another system, called the Polar coordinate system based on an angle and the distance from the center of a map, is much better suited for this.
Introduction
The problem with this working in the Polar system is that you need to convert your results to the Cartesian system, because Roblox operates in it. This is actually easy enough to do, if you have a formula in the Polar system. Let's take the Quadrifolium from Wikipedia. Its polar equation is:


r = math.cos(2*theta)
So, to obtain the values for x and z, we have to multiply r as follows:
x = r * math.cos(theta)
z = r * math.sin(theta)
We now get:
x=math.cos(2*i) * math.cos(theta)
z=math.cos(2*i) * math.sin(theta)
You will see these formulas again in the script below.
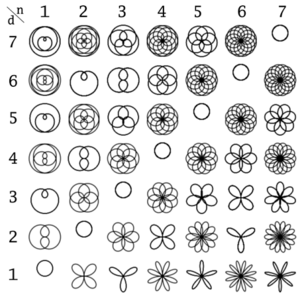
local n=2
local d=1
local k = n/d
for i = 1, 500, 1 do
local x=math.cos(k*i) * math.cos(i)
local z=math.cos(k*i) * math.sin(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
Other curves can be set by changing the value of n and d, which in turn result in a change in k.
Archimedean spiral
This classic mathematical example has a polar formula of:
r = a + b*theta
Similarly, using these conversion formulas, one arrives at the formulas used in the script further below:
x = r*cos(theta) -- #1
y = r*sin(theta) -- #2

local a = 1
local b = 1
for i = 1, 50, 0.1 do
local x = (a+b*(i)) * math.cos(i)
local z = (a+b*(i)) * math.sin(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
3-D images
Similarly, 3-D images can be created with a system similar to polar equations, called Spherical coordinates. The formula for a sphere in polar is rho = R. Using the formula to convert Spherical coordinates to Cartesian:
x = r * math.sin(theta) * math.cos(phi)
y = r * math.sin(theta) * math.sin(phi)
z = r * math.cos(theta)
The formula rho = R is obvious below.

local R=4
for i = 1,10, 1 do
for j = 1,10, .1 do
local x = R*math.sin(i)*math.cos(j)
local y = R*math.sin(i)*math.sin(j)
local z = R*math.cos(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
end
Ellipsoids
Another example is the ellipsoid, very similar to the sphere above. Really all that's being changed are the radii (a, b, and c).
Spherical formula:
x = a*math.cos(theta)*math.sin(phi)
y = b*math.sin(theta)*math.sin(phi)
z = math.cos(phi)
Conversion:
x = r*math.sin(theta)*math.cos(phi)
y = r*math.sin(theta)*math.sin(phi)
z = r*math.cos(theta)
Cartesian formula:
x = a*math.sin(i)*math.cos(j)
y = b*math.sin(i)*math.sin(j)
z = c*math.cos(i)

local a=3 -- radius
local b=10 -- radius
local c=5 -- radius
for i = 1, 50, 1 do
for j = 1, 50, 1 do
local x = a*math.sin(i)*math.cos(j)
local y = b*math.sin(i)*math.sin(j)
local z = c*math.cos(i)
local p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(30*x, 30*y, 30*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
end
By changing the values of a, b, and c, you can come up with different shapes:
a=b=c: Sphere
a=b>c: Oblate spheroid (disk-shaped)
a=b<c: Prolate spheroid (egg-shaped)
a>b>c: Scalene ellipsoid ("three unequal sides")