Parametric equations
Introduction
This tutorial will cover the basic notion of parametric equations, and how they apply to ROBLOX. Be careful with some of these scripts, they may lag your computer or cause it to freeze for a few moments or minutes.
Mathematical Functions and graphs
In algebra, you may be familiar with how a function is described with y on one side of the equals sign, and x on the other. For example:
y = x y = x^2 y = x + 3
and so on.
There are other ways of describing functions, that do the exact same thing. For example, with the equation
y = x^2
we can also describe both y and x in terms of a third variable:
x = t y = t^2
This does the exact same thing as y=x^2
Similarly, this works for more complex equations such as 2-D circles, spheres, etc:
The more familiar {{{1}}} equation for a circle now becomes:
x = a*cos(t) y = a*sin(t)
How does this help me?
In ROBLOX, while you are scripting, you need to define the x, y, and z coordinates for the bricks you are graphing. With parametric equations, you are given a formula for each x, y, and z coordinate. All you have to do now is just input these formulae in a way that ROBLOX understands, and you can make some very fancy things.
Making a grapher
local p = Instance.new("Part")
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.BrickColor = BrickColor.Black()
p.FormFactor = "Custom"
p.Size = Vector3.new(1, 1, 1)
function graph(bounds, f)
bounds.step = bounds.step or (bounds.max - bounds.min) / bounds.n
for t = bounds.from, bounds.to, bounds.step do
local xyz = f(t)
local p = p.clone()
p.CFrame = CFrame.new(xyz)
p.Parent = game.Workspace
end
end
What can I make with this?
Take a look at the article on Butterfly curves on MathWorld. You can make that fancy butterfly with a very short script, because they have given you all the formulae you need.

graph({from = 0, to = math.pi * 24, n = 1000}, function(t)
return Vector3.new(
10 * math.sin(t) * (math.exp(1)^math.cos(t) - 2*math.cos(4*t) - math.sin(t/12)^5),
10 * math.cos(t) * (math.exp(1)^math.cos(t) - 2*math.cos(4*t) - math.sin(t/12)^5),
0
)
end)
Deltoid curve
Other curves and shapes which would have been difficult to plot before become very simple. For example, the Deltoid curve:

graph({from = 0, to = math.pi * 2, n = 1000}, function(t)
return 100 * Vector3.new(
2 * math.cos(i) + math.cos(2*i),
2 * math.sin(i) - math.sin(2*i),
0
)
end)
As you can see here, too, the Parametric equations for x and y have been changed very little. I have chosen the value for z to be 0 because it is a constant -- in other words, it doesn't change. You can change the 100 to make the entire deltoid larger or smaller -- i.e., a value of 50 makes the deltoid smaller, a value of 150 makes it larger.
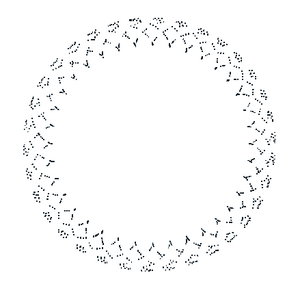
Epicycloids
There is an entire group of curves that can be made as "Epicycloids". The image shown below uses the value of k=7.2. Here, as well, the parametric equations can be plugged directly into Roblox:
function epicycloid(k)
return function(t)
return 100 * Vector3.new(
(k + 1) * math.cos(t) - math.cos((k + 1) * t),
(k + 1) * math.sin(t) - math.sin((k + 1) * t),
0
)
end
end
graph({from = 0, to = math.pi * 24, n = 1000}, epicycloid(7.2))
Hypocycloids

Similarly, there is a class of curves known as Hypocycloids
The above image is with the value of k=3.8. Wikipedia has several values and images on display with which to experiment.
for i = 0,100, .1 do
k=3.8
x=(k-1)*math.cos(i)+math.cos((k-1)*i)
y=(k-1)*math.sin(i)-math.sin((k-1)*i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100*y, 100))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26)
end
Hypotrochoids
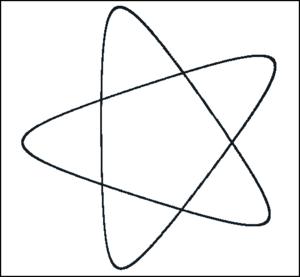
Hypotrochoids are another example of curves that can be scripted with parametric equations. Here, the x and y formula are just as from wikipedia... and all you need to set are the values for R, r, and d (in this example the values have been provided by wikipedia!)
for i = 0,360, 1 do
R=5.0
r=3
d=5
x=((R-r)*math.cos(i))+d*math.cos(((R-r)/r)*i)
y=((R-r)*math.sin(i))-d*math.sin(((R-r)/r)*i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100*y, 100))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26)
end
Limaçon trisectrix
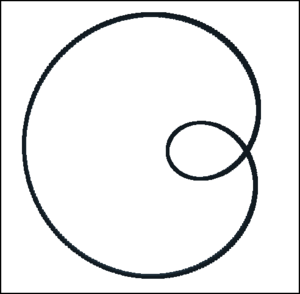
The Limaçon trisectrix is a special instance of the trisectrix of Pascal (also called the limaçon of Pascal). Here, again, once you get the basic formula down, you can have a wide variety of curves with different values inserted into a and b.
for i = 0,360, 1 do
a=4
b=2
x=(a/2)+b*math.cos(i)+(a/2)*math.cos(2*i)
y=b*math.sin(i)+(a/2)*math.sin(2*i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100*y, 100))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26)
end
Lissajous curve

"A Lissajous curve is the graph of the system of parametric equations
x=A*sin(at+δ), y=B*sin(bt) which describes complex harmonic motion."
for i = 1,1500, .5 do
A=1
B=1
a=9
b=8
phi=2
x=A*math.sin(a*i+phi)
z=B*math.sin(b*i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1000*x, 100, 1000*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
3D Curves
Viviani's curve

for t = 0,4*math.pi, .1 do
a=2
b=1
x=a*(1+math.cos(t))
y=math.sin(t)
z=2*math.sin(t/2)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26)
end
Clélies Curves
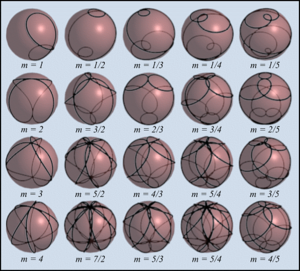

for t = 0,4*math.pi, .05 do
a=4 -- radius
m=4/5
x = a * math.sin(m*t)*math.cos(t)
y = a * math.sin(m*t)*math.sin(t)
z = a * math.cos(m*t)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26)
end
Tornado
Ever wanted to know how to make a tornado like the tornado hat?

for i = 1,15, .1 do
x=i*math.cos(i)
y=i
z=i*math.sin(i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26) -- change this to whatever color you want
end

for t = 1,20, .01 do
x=2*math.sin(3*t)*math.cos(t)
y=2*math.sin(3*t)*math.sin(t)
z=math.sin(3*t)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26) -- change this to whatever color you want
end

for t = 1,20, .01 do
x=3*math.cos(t)+math.cos(10*t)*math.cos(t)
y=math.sin(10*t)
z=3*math.sin(t)+math.cos(10*t)*math.sin(t)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26) -- change this to whatever color you want
end
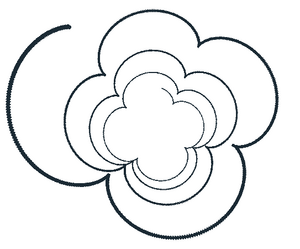
for t = 1,25, .01 do
x=5*math.cos(t)-math.cos(5*t)
y=t
z=5*math.sin(t)-math.sin(5*t)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(10*x, 10*y, 10*z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(26) -- change this to whatever color you want
end
Loxodromes

You can alter the number of loops by altering the a value.
for t = 1,500, 1 do
a=2
x=math.cos(t) *math.cos (1/math.tan (a*t))
y=math.sin(t) *math.cos (1/math.tan (a*t))
z= -math.sin (1/math.tan (a*t))
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100*y, 100*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
See Also
MathWorld, Parametric Equations