Polar equations: Difference between revisions
>Mindraker mNo edit summary |
>Mindraker No edit summary |
||
| Line 24: | Line 24: | ||
for i = 1,500, 1 do | for i = 1,500, 1 do | ||
x=math.cos( | n=2 | ||
z=math.cos( | d=1 | ||
k = n/d | |||
x=math.cos(k*i) * math.cos(i) | |||
z=math.cos(k*i) * math.sin(i) | |||
p = Instance.new("Part") | p = Instance.new("Part") | ||
| Line 38: | Line 43: | ||
end | end | ||
</pre> | </pre> | ||
[[Image:Polar2.PNG|thumb|k=3/2]] | |||
<pre> | |||
for i = 1,500, 1 do | |||
n=3 | |||
d=2 | |||
k = n/d | |||
x=math.cos(k*i) * math.cos(i) | |||
z=math.cos(k*i) * math.sin(i) | |||
p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z)) | |||
p.Size = Vector3.new(8,8,8) | |||
p.Anchored = true | |||
p.BottomSurface = "Smooth" | |||
p.TopSurface = "Smooth" | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | |||
</pre> | |||
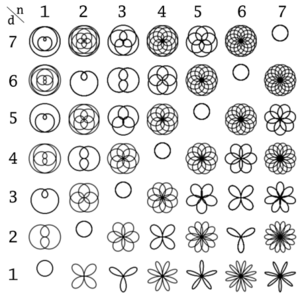
[[Image:Rhodonea curve.png|thumb|Rhodonea curves]] | |||
Other curves can be set by changing the value of k, as seen in the table. | |||
== See also == | == See also == | ||
| Line 43: | Line 77: | ||
[http://en.wikipedia.org/wiki/Quadrifolium Wikipedia, Quadrifolium] | [http://en.wikipedia.org/wiki/Quadrifolium Wikipedia, Quadrifolium] | ||
[http://en.wikipedia.org/wiki/Rose_(mathematics) Rose curve] | |||
[[Category:Scripting Tutorials]] | [[Category:Scripting Tutorials]] | ||
Revision as of 18:36, 30 December 2008
Introduction
Roblox operates using the Cartesian coordinate system. This is a gridlike system much like the tiles on the floor of a bathroom. This system is ideal for certain things, e.g., straight lines, roads, buildings, tiles. It is not as good for other things, such as spirals. Another system, called the Polar coordinate system based on an angle and the distance from the center of a map, is much better suited for this.
The problem with this is that you need to convert from the Polar system to the Cartesian system, because Roblox operates in the Cartesian system. This is actually easy enough to do, if you have a formula in the Polar system. Let's take the Quadrifolium from Wikipedia. Its polar equation is:
r=math.cos(2*θ)
So, to obtain the values for x and z, we have to multiply r as follows:
x = r * math.cos(θ)
z = r * math.sin(θ)
We now get:
x=math.cos(2*i) * math.cos(θ)
z=math.cos(2*i) * math.sin(θ)
You will see these formulas again in the script below.

for i = 1,500, 1 do
n=2
d=1
k = n/d
x=math.cos(k*i) * math.cos(i)
z=math.cos(k*i) * math.sin(i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end

for i = 1,500, 1 do
n=3
d=2
k = n/d
x=math.cos(k*i) * math.cos(i)
z=math.cos(k*i) * math.sin(i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*x, 100, 100*z))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
Other curves can be set by changing the value of k, as seen in the table.