User:Outofspace/Shape Scripts: Difference between revisions
>Outofspace m added mon4.png |
>Outofspace No edit summary |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
[[Image:OosAward.PNG|thumb|Best of "I accidentally invented" award.]] | [[Image:OosAward.PNG|thumb|Best of "I accidentally invented" award.]] | ||
=== | === Sphere's === | ||
More of Minraker's scripts I've tampered with. | |||
This one is AWESOME. | |||
<pre> | <pre> | ||
for i = 0,25, 1 do | |||
for j = 0,25, 1 do | |||
for | |||
p = Instance.new("Part") | p = Instance.new("Part") | ||
p. | p.CFrame = CFrame.new(Vector3.new(100*math.sin(i), (100*math.sin(i)*math.cos(j))+100, 100*math.sin(i)*math.sin(j))) | ||
p.Size = Vector3.new(8,8,8) | |||
p. | |||
p.Anchored = true | p.Anchored = true | ||
p.Color = Color3.new(1) | p.Color = Color3.new(1) | ||
wait( | p.BottomSurface = "Smooth" | ||
p.TopSurface = "Smooth" | |||
p.Parent = game.Workspace | |||
wait() | |||
end | |||
end | end | ||
</pre> | </pre> | ||
| Line 65: | Line 60: | ||
wait(0.5) | wait(0.5) | ||
end | end | ||
</pre> | |||
A cool variation of the double helix scripts that acts as stairs: | |||
<pre> | |||
--Best when "wait()" is used. | |||
--Makes for a awesome effect! | |||
local i = 0 | |||
for i = 0, 100, .1 do | |||
local p = Instance.new("Part") | |||
p.Parent = game.Workspace | |||
p.Name = "Brick" | |||
p.Size = Vector3.new(14,1,14) | |||
p.Anchored = true | |||
p.Position=Vector3.new(100*math.cos(i), 17*i, 150*math.sin(i)) | |||
local p = Instance.new("Part") | |||
p.Parent = game.Workspace | |||
p.Name = "Brick" | |||
p.Size = Vector3.new(14,1,14) | |||
p.Anchored = true | |||
p.Position=Vector3.new(-100*math.sin(i), 17*i, 150*math.cos(i)) | |||
wait() | |||
end | |||
</pre> | </pre> | ||
| Line 281: | Line 300: | ||
wait(0.5) | wait(0.5) | ||
end | |||
</pre> | |||
== Others == | |||
I have determined that that the top 3 variables control spacing and height. The "25" and "2.5" are proportions that make for a good square. The proportion is (where 25 = a, and 2.5 = b) b = a/10. Here is everything else. "a" controls the number of blocks that will span top-to-bottom, and "b" controls the space between them. The amount of blocks withing the shape s determined by both "a" and "b". Each resulting "block" that the bricks make up, will be twice as dense if you had douled "a" and not "b". The result is a cube proportional to the original; it would be twice as dense and twice as large. With that in mind, you could easily control width of the resulting block, with "b". If you had doubled "b" with "a", the result would be bricks more spread out, and not as dense. It would be a perfect proportion. Here are some examples: | |||
<pre> | |||
for i = 1, 25, 2.5 do | |||
for j = 1, 25, 2.5 do | |||
for k = 1, 25, 2.5 do | |||
p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(i,j,k)) | |||
p.Size = Vector3.new(1,1,1) | |||
p.Anchored = true | |||
p.Color = Color3.new(1) | |||
p.formFactor = "Symmetric" | |||
p.Parent = game.Workspace | |||
wait(.1) | |||
end | |||
end | |||
end | |||
</pre> | |||
This next one creates a slope. | |||
<pre> | |||
for i = 1, 50, 2.5 do | |||
for k = 1, 50, 2.5 do | |||
p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(i,i,k)) | |||
p.Size = Vector3.new(1,1,1) | |||
p.Anchored = true | |||
p.Color = Color3.new(1) | |||
p.formFactor = "Symmetric" | |||
p.Parent = game.Workspace | |||
--wait() | |||
end | |||
end | |||
</pre> | |||
Here's something cool: | |||
<pre> | |||
for i = 1, 25, 2.5 do | |||
for j = 1, 25, 2.5 do | |||
for k = 1, 25, 2.5 do | |||
i=i + 4 | |||
k=k + 4 | |||
j=math.cos(i) + 4 | |||
p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(i,j,k)) | |||
p.Size = Vector3.new(1,1,1) | |||
p.Anchored = true | |||
p.Color = Color3.new(1) | |||
p.formFactor = "Symmetric" | |||
p.Parent = game.Workspace | |||
wait() | |||
end | |||
end | |||
end | |||
</pre> | |||
Waves | |||
<pre> | |||
for i = 1, 25, .5 do | |||
for j = 1, 25, .5 do | |||
for k = 1, 25, .5 do | |||
i=i +4 | |||
k=k + 4 | |||
j=j + math.cos(k) | |||
p = Instance.new("Part") | |||
p.CFrame = CFrame.new(Vector3.new(i,j,i)) | |||
p.Size = Vector3.new(1,1,1) | |||
p.Anchored = true | |||
p.Color = Color3.new(1) | |||
p.formFactor = "Symmetric" | |||
p.Parent = game.Workspace | |||
wait() | |||
end | |||
end | |||
end | end | ||
</pre> | </pre> | ||
Latest revision as of 11:16, 29 December 2008
The Shape Scripts
Accidents occur:
Sphere's
More of Minraker's scripts I've tampered with.
This one is AWESOME.
for i = 0,25, 1 do
for j = 0,25, 1 do
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(100*math.sin(i), (100*math.sin(i)*math.cos(j))+100, 100*math.sin(i)*math.sin(j)))
p.Size = Vector3.new(8,8,8)
p.Anchored = true
p.Color = Color3.new(1)
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
wait()
end
end
Stair Maker
Ok, this was useful once.
x = 1
xx = 1
xxx = 1
for i=1,10 do --Replace 10 with the number of steps you want.
local a = Instance.new("Part")
a.Parent = game.Workspace
a.Anchored = true
a.Locked = true
--y = x+5*10/3
yy = xx+10*10/4
yyy = xxx+15*10/8
a.Position = Vector3.new(y, yy, yyy)
z = x + 1
zz = xx + 1
zzz = xxx + 1
x = z
xx = zz
xxx = zzz
wait(0.5)
end
A cool variation of the double helix scripts that acts as stairs:
--Best when "wait()" is used.
--Makes for a awesome effect!
local i = 0
for i = 0, 100, .1 do
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(14,1,14)
p.Anchored = true
p.Position=Vector3.new(100*math.cos(i), 17*i, 150*math.sin(i))
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(14,1,14)
p.Anchored = true
p.Position=Vector3.new(-100*math.sin(i), 17*i, 150*math.cos(i))
wait()
end
Random
Looks like a tree.
x = 1
xx = 1
xxx = 1
for i=1,25 do --Replace 10 with the number of steps you want.
local a = Instance.new("Part")
a.Parent = game.Workspace
--a.Anchored = true
--a.Locked = true
y = x+5*-10/3
yy = xx+6*-10/4
yyy = xxx+7*-10/5
--a.Position = Vector3.new(y, yy, yyy)
a.Size = Vector3.new(y, yy, yyy)
z = x + 1
zz = xx + 2
zzz = xxx + 3
x = z
xx = zz
xxx = zzz
wait(0.5)
end
Double Helix
Thanks again to Mindraker, for providing the original script (which will now be dissected.)
The following was made by accident...rofl...
local i = 0
for i = 0, 250, .1 do
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(11,1,11)
p.Anchored = true
p.Position=Vector3.new(100*math.cos(i), 15*i, 10*math.sin(i))
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(11,1,11)
p.Anchored = true
p.Position=Vector3.new(-100*math.sin(i), 15*i, 10*math.cos(i))
wait()
end
One that acts as stairs:
local i = 0
for i = 0, 100, .1 do
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(11,1,11)
p.Anchored = true
p.Position=Vector3.new(100*math.cos(i), 15*i, 20*math.sin(i))
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(11,1,11)
p.Anchored = true
p.Position=Vector3.new(-100*math.sin(i), 15*i, 20*math.cos(i))
wait()
end
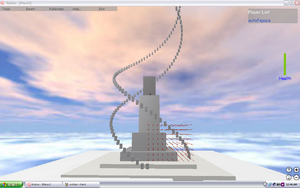
Even crazier...
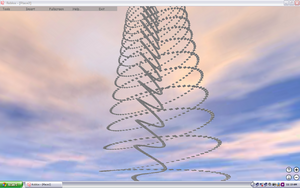
local i = 0
for i = 0, 100, .1 do
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(11,1,11)
p.Anchored = true
p.Position=Vector3.new(100*math.cos(i), 15*i, 250*math.sin(i))
local p = Instance.new("Part")
p.Parent = game.Workspace
p.Name = "Brick"
p.Size = Vector3.new(11,1,11)
p.Anchored = true
p.Position=Vector3.new(-100*math.sin(i), 15*i, 10*math.cos(i))
wait()
end
Quadrilateral...thing
I forgot the name of the shape.
x = 1
xx = 1
xxx = 1
for i=1,25 do --Replace 10 with the number of steps you want.
local a = Instance.new("Part")
a.Parent = game.Workspace
a.Anchored = true
--a.Locked = true
y = x+5^1*10*1/2^1-400
yy = xx+5^2*10*2/2^2-400
yyy = xxx+5^3*10*3/2^3-400
--a.Position = Vector3.new(y, yy, yyy)
a.Size = Vector3.new(y, yy, yyy)
z = x + 1
zz = xx + 1
zzz = xxx + 1
x = z
xx = zz
xxx = zzz
wait(0.1)
end
Mountain
Slightly more successful. It's a modified version of his script.
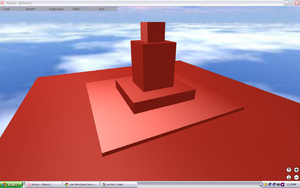
x=1
y=1
for i = 1, 10 do
x=x+x
y=x + 2 * 4 /3
z=y^2 / 4
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,1.8,1))
p.Size = Vector3.new(x,z,y)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
wait(0.5)
end
Here's a variation of it:
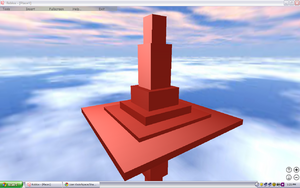
x=1
y=1
for i = 1, 10 do
x=x + 2 + x * 5 / 10
y=x + 2 * 4 /3
z=y^2 / 3
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,1.8,1))
p.Size = Vector3.new(x,z,y)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
wait(0.5)
end
Click here for a copy!. Here's the terrain script (2nd Variation):
x=1
y=1
for i = 1, 10 do
x=x+x + 60 / 20
y=x +1
z=y ^ 2 / 3
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,1.8,1))
p.Size = Vector3.new(x,z,y)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
wait(0.5)
end
Others
I have determined that that the top 3 variables control spacing and height. The "25" and "2.5" are proportions that make for a good square. The proportion is (where 25 = a, and 2.5 = b) b = a/10. Here is everything else. "a" controls the number of blocks that will span top-to-bottom, and "b" controls the space between them. The amount of blocks withing the shape s determined by both "a" and "b". Each resulting "block" that the bricks make up, will be twice as dense if you had douled "a" and not "b". The result is a cube proportional to the original; it would be twice as dense and twice as large. With that in mind, you could easily control width of the resulting block, with "b". If you had doubled "b" with "a", the result would be bricks more spread out, and not as dense. It would be a perfect proportion. Here are some examples:
for i = 1, 25, 2.5 do
for j = 1, 25, 2.5 do
for k = 1, 25, 2.5 do
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(i,j,k))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.formFactor = "Symmetric"
p.Parent = game.Workspace
wait(.1)
end
end
end
This next one creates a slope.
for i = 1, 50, 2.5 do
for k = 1, 50, 2.5 do
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(i,i,k))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.formFactor = "Symmetric"
p.Parent = game.Workspace
--wait()
end
end
Here's something cool:
for i = 1, 25, 2.5 do
for j = 1, 25, 2.5 do
for k = 1, 25, 2.5 do
i=i + 4
k=k + 4
j=math.cos(i) + 4
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(i,j,k))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.formFactor = "Symmetric"
p.Parent = game.Workspace
wait()
end
end
end
Waves
for i = 1, 25, .5 do
for j = 1, 25, .5 do
for k = 1, 25, .5 do
i=i +4
k=k + 4
j=j + math.cos(k)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(i,j,i))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.formFactor = "Symmetric"
p.Parent = game.Workspace
wait()
end
end
end