Derivatives: Difference between revisions
>Mindraker Something is wrong with this |
>NXTBoy No edit summary |
||
| (35 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
==Goal== | |||
This page will help smooth out your [[Terrain Generation|Terrains]], if you use mathematical formulae to create them. In ROBLOX, however, we do not work with mathematical "points", but "bricks", which occupy space. Therefore, in order to smooth out terrains and functions, you will want to know the slopes of your functions... to know the slopes of your terrains. | This page will help smooth out your [[Terrain Generation|Terrains]], if you use mathematical formulae to create them. In ROBLOX, however, we do not work with mathematical "points", but "bricks", which occupy space. Therefore, in order to smooth out terrains and functions, you will want to know the slopes of your functions... to know the slopes of your terrains. | ||
[[Image:Derivative.PNG|thumb|An example of how you can use Derivatives]] | [[Image:Derivative.PNG|thumb|150px|An example of how you can use Derivatives]] | ||
==Introduction== | |||
A derivative is the slope of a function, or, phrased differently, the difference in the height divided by the difference in width at that point. | A derivative is the slope of a function, or, phrased differently, the difference in the height divided by the difference in width at that point. | ||
The [[Ramps]] article provides a method on how to rotate a brick: | The [[Ramps]] article provides a method on how to rotate a brick: | ||
{{lua|= | |||
game.Workspace.slope.CFrame=CFrame.new(Vector3.new(0,100,0)) * CFrame.fromAxisAngle(Vector3.new(0,0,1), math.pi/2) | game.Workspace.slope.CFrame = CFrame.new(Vector3.new(0, 100, 0)) | ||
* CFrame.fromAxisAngle(Vector3.new(0, 0, 1), math.pi / 2) | |||
}} | |||
Here we have the brick being created in its position in the first CFrame, and the rotation in the second CFrame. This is where the derivative comes in. In the script below, z=-x^2. The derivative for this is -2*x | Here we have the brick being created in its position in the first CFrame, and the rotation in the second CFrame. This is where the derivative comes in. In the script below, z=-x^2. The derivative for this is -2*x. (Why does -x work better than -2*x???) | ||
{{lua|= | |||
x | function f(x) return -x^2 end | ||
function f_derivative(x) return 2*x end | |||
x | |||
for x = -1.8, 1.8, .01 do | |||
local y = f(x) | |||
local dydx = f_derivative(x) | |||
local slopeAngle = math.atan(dydx) | |||
local p = Instance.new('Part') | |||
p.CFrame = CFrame.new(100 * Vector.new(x, y, 0)) | |||
* CFrame.fromAxisAngle(Vector3.new(0, 0, 1), slopeAngle) | |||
p.Size = Vector3.new(1, 10, 1) | |||
p.Anchored = true | |||
p.BottomSurface = 'Smooth' | |||
p.TopSurface = 'Smooth' | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | end | ||
</pre> | </pre>}} | ||
You can smooth out trigonometric functions, too. | |||
[[Image:Derivative2.PNG|thumb|150px|Sin wave (yes, it's flipped around)]] | |||
{{Example|<pre> | |||
function f(x) return math.sin(x) end | |||
function f_derivative(x) return math.cos(x) end | |||
for x = -2.5, 2.5, .01 do | |||
local y = f(x) | |||
local dydx = f_derivative(x) | |||
local slopeAngle = math.atan(dydx) | |||
local p = Instance.new('Part') | |||
p.CFrame = CFrame.new(Vector3.new(10 * x, 10 * y, 10)) * CFrame.fromAxisAngle(Vector3.new(0, 0, 1), slopeAngle) | |||
--cos is the derivative of sin | |||
-- | |||
p.Size = Vector3.new(1,1,1) | |||
p.Anchored = true | |||
p.BottomSurface = 'Smooth' | |||
p.TopSurface = 'Smooth' | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | end | ||
</pre> | </pre>}} | ||
==3D Terrain== | |||
[[Image:Smooth.PNG|thumb|150px|Smoothed out 3D terrain]] | |||
This is the sinx+siny formula from [[Terrain Generation]], only smoothed out now. (This needs to be double checked.) | |||
{{Example|<pre> | |||
local x, y = 0, 0 | |||
for i = -2,2, .1 do | |||
for j = -2,2, .1 do | |||
y = math.sin(i) + math.sin(j) -- here is the formula | |||
local p = Instance.new('Part') | |||
p.CFrame=CFrame.new(Vector3.new(10 * i, 10 * y, 10 * j)) * CFrame.fromAxisAngle(Vector3.new(0, 0, 1), math.cos(i) + math.cos(j)) | |||
p.Size = Vector3.new(1,1,1) | |||
p.Anchored = true | |||
p.BottomSurface = "Smooth" | |||
p.TopSurface = "Smooth" | |||
p.Parent = game.Workspace | |||
p.BrickColor = BrickColor.new(217) | |||
end | |||
end | |||
</pre>}} | |||
[http://en.wikipedia.org/wiki/Derivative Wikipedia article on Derivatives] | ==See Also== | ||
*[[Ramps]] | |||
*[[Terrain Generation]] | |||
*[http://en.wikipedia.org/wiki/Derivative Wikipedia article on Derivatives] | |||
[[Category:Scripting Tutorials]] | [[Category:Scripting Tutorials]] | ||
[[Category:Mathematical Methods]] | |||
Latest revision as of 13:31, 11 March 2012
Goal
This page will help smooth out your Terrains, if you use mathematical formulae to create them. In ROBLOX, however, we do not work with mathematical "points", but "bricks", which occupy space. Therefore, in order to smooth out terrains and functions, you will want to know the slopes of your functions... to know the slopes of your terrains.
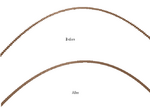
Introduction
A derivative is the slope of a function, or, phrased differently, the difference in the height divided by the difference in width at that point.
The Ramps article provides a method on how to rotate a brick:
game.Workspace.slope.CFrame = CFrame.new(Vector3.new(0, 100, 0))
* CFrame.fromAxisAngle(Vector3.new(0, 0, 1), math.pi / 2)
Here we have the brick being created in its position in the first CFrame, and the rotation in the second CFrame. This is where the derivative comes in. In the script below, z=-x^2. The derivative for this is -2*x. (Why does -x work better than -2*x???)
function f(x) return -x^2 end
function f_derivative(x) return 2*x end
for x = -1.8, 1.8, .01 do
local y = f(x)
local dydx = f_derivative(x)
local slopeAngle = math.atan(dydx)
local p = Instance.new('Part')
p.CFrame = CFrame.new(100 * Vector.new(x, y, 0))
* CFrame.fromAxisAngle(Vector3.new(0, 0, 1), slopeAngle)
p.Size = Vector3.new(1, 10, 1)
p.Anchored = true
p.BottomSurface = 'Smooth'
p.TopSurface = 'Smooth'
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
</pre>
You can smooth out trigonometric functions, too.

function f(x) return math.sin(x) end
function f_derivative(x) return math.cos(x) end
for x = -2.5, 2.5, .01 do
local y = f(x)
local dydx = f_derivative(x)
local slopeAngle = math.atan(dydx)
local p = Instance.new('Part')
p.CFrame = CFrame.new(Vector3.new(10 * x, 10 * y, 10)) * CFrame.fromAxisAngle(Vector3.new(0, 0, 1), slopeAngle)
--cos is the derivative of sin
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.BottomSurface = 'Smooth'
p.TopSurface = 'Smooth'
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
3D Terrain

This is the sinx+siny formula from Terrain Generation, only smoothed out now. (This needs to be double checked.)
local x, y = 0, 0
for i = -2,2, .1 do
for j = -2,2, .1 do
y = math.sin(i) + math.sin(j) -- here is the formula
local p = Instance.new('Part')
p.CFrame=CFrame.new(Vector3.new(10 * i, 10 * y, 10 * j)) * CFrame.fromAxisAngle(Vector3.new(0, 0, 1), math.cos(i) + math.cos(j))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.BottomSurface = "Smooth"
p.TopSurface = "Smooth"
p.Parent = game.Workspace
p.BrickColor = BrickColor.new(217)
end
end