Fractals: Difference between revisions

From Legacy Roblox Wiki
Jump to navigationJump to search
← Older edit
VisualWikitext
>Mindraker
Flat images... there! That looks a lot better.
>Mindraker
No edit summary
 
(48 intermediate revisions by the same user not shown)
Line 33: Line 33:
p.Parent = game.Workspace
p.Parent = game.Workspace
--wait(.1)
--wait(.1)
end
</pre>
== 3D Sierpinsky Triangle ==
[[Image:3D Sierpinsky Triangle.PNG|thumb|3D Sierpinsky Triangle]]
<b>WARNING</b> This can freeze up your computer.  (My computer could only handle 5000 after about a <b>half hour</b>.)  If you have a slow computer, reduce the "For" loop to a lower number, like 500, then work your way up to 1000.
For a better picture of what this is, see the [http://en.wikipedia.org/wiki/Sierpi%C5%84ski_Triangle wikipedia article on Sierpinsky triangles]
<pre>
local x = 0
local y = 1.8
local z = 0
for i = 1, 5000 do
a = math.random(1,8)
if a == 1 then
x = (x - 200)/2
y = (y - 200)/2
z = (z + 200)/2
end
if a == 2 then
x = (x + 200)/2
y = (y - 200)/2
z = (z + 200)/2
end
if a == 3 then
x = (x - 200)/2
y = (y - 200)/2
z = (z - 200)/2
end
if a == 4 then
x = (x + 200)/2
y = (y - 200)/2
z = (z - 200)/2
end
if a == 5 then
x = (x + 0)/2
y = (y + 200)/2
z = (z + 0)/2
end
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,y,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end
</pre>
== Sierpinksy ==
[[Image:Srpnskythree.PNG|thumb|Sierpinsky]]
This won't make a mathematical recreation of the Sierpinksy fractal, but it will merely make a pretty visual representation of it.
<pre>
x=1
y=1
for i = 50, 1, -1 do
x=i
y=(50-i)
z=(50-i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,i,1))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)
end
for i = 50, 1, -1 do
x=i
y=(50-i)
z=(50-i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+50,i,1+50))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)
end
for i = 50, 1, -1 do
x=i
y=(50-i)
z=(50-i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+50,i,1))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)
end
for i = 50, 1, -1 do
x=i
y=(50-i)
z=(50-i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,i,1+50))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)
end
for i = 50, 1, -1 do
x=i
y=(50-i)
z=(50-i)
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+25,i+50,1+25))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)
end
end
</pre>
</pre>
Line 76: Line 224:
p.Parent = game.Workspace
p.Parent = game.Workspace
wait(.1)
wait(.1)
end
</pre>
== Mandelbrot set ==
[[Image:Mandelbrot.PNG|thumb|Mandelbrot set]]
This image requires the [[Output|Output window]] of Roblox studio.  Thanks to [http://severinghaus.org/sites/severinghaus.org/files/luabrot.lua Serveringhaus.org] for this code.
<pre>
iter=100
esclim=2.0
ulx=-2.0
uly=1.0
lrx=1.0
lry=-1.0
width=70
height=40
function abs(x,y)
    return math.sqrt(x*x+y*y)
end
function escapeq(cx,cy)
    local zx=0.0
    local zy=0.0
    local i=0
    while i<iter and abs(zx,zy)<esclim do
        tmp=zx*zx-zy*zy
        zy=2.0*zx*zy
        zx=tmp
        zx=zx+cx
        zy=zy+cy
        i=i+1
    end
    return i<iter
end
for y=1,height do
    line=''
    for x=1,width do
        zx=ulx+(lrx-ulx)/width*x;
        zy=uly+(lry-uly)/height*y;
        if escapeq(zx,zy) then
            line=line..'.'
        else
            line=line..'#'
        end
    end
    print(line);
end
</pre>
== Mandelbrot Brick Set ==
[[Image:Mandelbrot2.PNG|thumb|Brick version of the Mandelbrot Fractal]]
This is almost identical to the script above, but it uses bricks instead of the [[Output|Output menu]].
<pre>
iter=100
esclim=2.0
ulx=-2.0
uly=1.0
lrx=1.0
lry=-1.0
width=70
height=40
function abs(x,y)
    return math.sqrt(x*x+y*y)
end
function escapeq(cx,cy)
    local zx=0.0
    local zy=0.0
    local i=0
    while i<iter and abs(zx,zy)<esclim do
        tmp=zx*zx-zy*zy
        zy=2.0*zx*zy
        zx=tmp
        zx=zx+cx
        zy=zy+cy
        i=i+1
    end
    return i<iter
end
for y=1,height do
    for x=1,width do
        zx=ulx+(lrx-ulx)/width*x;
        zy=uly+(lry-uly)/height*y;
        if escapeq(zx,zy) then
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,y))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
        else
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,y))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
--p.Color = Color3.new(2)
p.Parent = game.Workspace
--wait(.1)
        end
    end
end
end
</pre>
</pre>
Line 118: Line 382:
--wait(.1)
--wait(.1)
end
end
</pre>
== 3D Cantor set ==
[[Image:3d cantor set2.PNG|thumb|3D Cantor set]]
<b>WARNING</b> This can freeze up your computer.  If you have a slow computer, reduce the "For" loop to a lower number, like 500, then work your way up to 1000.
<pre>
local x = 0
local y = 1.8
local z = 0
for i = 1, 2000 do
a = math.random(1,8)
if a == 1 then
x = (x - 250)/3
y = (y - 250)/3
z = (z - 250)/3
end
if a == 2 then
x = (x - 250)/3
y = (y - 250)/3
z = (z + 250)/3
end
if a == 3 then
x = (x - 250)/3
y = (y + 250)/3
z = (z - 250)/3
end
if a == 4 then
x = (x - 250)/3
y = (y + 250)/3
z = (z + 250)/3
end
if a == 5 then
x = (x + 250)/3
y = (y + 250)/3
z = (z + 250)/3
end
if a == 6 then
x = (x + 250)/3
y = (y - 250)/3
z = (z + 250)/3
end
if a == 7 then
x = (x + 250)/3
y = (y + 250)/3
z = (z - 250)/3
end
if a == 8 then
x = (x + 250)/3
y = (y - 250)/3
z = (z - 250)/3
end
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,y,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end
</pre>
== 3D Cantor set 2 ==
[[Image:3d cantor set3.PNG|thumb|3D Cantor set]]
This is a proportional representation of the 3D Cantor set.
<pre>
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17+66,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17+66,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17+66,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17+66,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
</pre>
</pre>


Line 205: Line 605:
x = (x - 350)/5
x = (x - 350)/5
z = (z + 5)/5
z = (z + 5)/5
end
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end
</pre>
== Quadratic Koch, 2nd iteration ==
[[Image:Quadratic Koch w script.PNG|thumb|Quadratic Koch, 3D (type 1), 2nd iteration]]
This doesn't get into the math behind it.  See [http://commons.wikimedia.org/wiki/File:Quadratic_Koch_3D_(type1).png wikipedia] for more info.
<pre>
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,16.2,0))
p.Size = Vector3.new(30,30,30)
p.Anchored = true
p.Color = Color3.new(0)
p.formFactor = "Symmetric"
p.Parent = game.Workspace
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,21,0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,16.2,20))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(21,16.2,0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-19,16.2,0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,16.2,-20))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,6.2,30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-29, 6.2, 0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0, 6.2, -30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(31, 6.2, 0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(31, 6.2, -30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-30, 6.2, -30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-29, 6.2, 30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(30, 6.2, 30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"
</pre>
== Vicsek Fractal ==
[[Image:Fractal28dec2008.PNG|thumb|I don't know why the middle is kicked off at an angle]]
<pre>
x = 50
y = 1.8
z = 50
for i = 1, 1000, 1  do
a = math.random(1,5)
if a == 1 then
x = .33*x - 66
z = .33*z + 66
end
if a == 2 then
x = .325*x +.325*z
z = -.325*x+.325*z
end
if a == 3 then
x = .33*x - 66
z = .33*z - 66
end
if a == 4 then
x = .33*x + 66
z = .33*z - 66
end
if a == 5 then
x = .33*x + 66
z = .33*z + 66
end
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end
</pre>
== Fractal from my old calculus book ==
I don't know the name of this one.  It's lopsided for some reason.
[[Image:Fractal28dec2008b.PNG|thumb|fractal from my old calculus book]]
<pre>
x = 50
y = 1.8
z = 50
for i = 1, 2000, 1  do
a = math.random(1,5)
if a == 1 then
x = (.25*x) - 25
z = .25*z + 25
end
if a == 2 then
x = .288*x -(.167*z) - 50
z = .167*x +.288*z - 50
end
if a == 3 then
x = (.25*x)-74.6
z = .25*z+74.6
end
if a == 4 then
x = .5*x+50
z = .5*z-50
end
if a == 5 then
x = .18*x+.174*z+50
z = (-.174*x)+.18*z+50
end
end


Line 220: Line 839:


[[Image:Cantor3d.PNG|200px|3D Cantor dust]] [[Image:Quadratic Koch 3D (type1 stage3).PNG|200px|Third iteration of 3D Koch quadratic fractal]] [[Image:Square koch 3.PNG|200px|Square koch 3]] <br>
[[Image:Cantor3d.PNG|200px|3D Cantor dust]] [[Image:Quadratic Koch 3D (type1 stage3).PNG|200px|Third iteration of 3D Koch quadratic fractal]] [[Image:Square koch 3.PNG|200px|Square koch 3]] <br>
[[Image:Sierpinskytriangle.PNG|200px|Sierpinsky triangle fractal]] [[Image:Snskytwo.PNG|200px|Variation of the Sierpinsky triangle fractal]] [[Image:Fractalx.PNG|200px|Vicsek fractal]] <br> [[Image:FractalT.PNG|200px|Fractal T]] [[Image:Fractal kite.PNG|200px|Fractal kite]]
[[Image:Sierpinskytriangle.PNG|200px|Sierpinsky triangle fractal]] [[Image:Snskytwo.PNG|200px|Variation of the Sierpinsky triangle fractal]] [[Image:Fractalx.PNG|200px|Vicsek fractal]]<br> [[Image:FractalT.PNG|200px|Fractal T]] [[Image:Fractal kite.PNG|200px|Fractal kite]]


== See Also ==
== See Also ==
Line 227: Line 846:


[http://www1.hollins.edu/homepages/hammerpw/SKMDAY/beauty.htm Beauty in Mathematics, an introductory article on fractals with helpful images]
[http://www1.hollins.edu/homepages/hammerpw/SKMDAY/beauty.htm Beauty in Mathematics, an introductory article on fractals with helpful images]
[[Category:Player Created]]

Latest revision as of 09:02, 29 December 2008

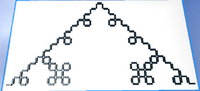
Sierpinsky Triangle

Sierpinksy Triangle
x = 0
y = 1.8
z = 0
for i = 1, 4000 do
a = math.random(1,3)

if a == 1 then 
x = x / 2
z = (z - 250)/2
end

if a == 2 then 
x = (x - 250)/2
z = (z + 250)/2
end

if a == 3 then 
x = (x + 250)/2
z = (z + 250)/2
end


p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

3D Sierpinsky Triangle

3D Sierpinsky Triangle

WARNING This can freeze up your computer. (My computer could only handle 5000 after about a half hour.) If you have a slow computer, reduce the "For" loop to a lower number, like 500, then work your way up to 1000.

For a better picture of what this is, see the wikipedia article on Sierpinsky triangles 

local x = 0
local y = 1.8
local z = 0

for i = 1, 5000 do
a = math.random(1,8)

if a == 1 then 
x = (x - 200)/2
y = (y - 200)/2
z = (z + 200)/2
end

if a == 2 then 
x = (x + 200)/2
y = (y - 200)/2
z = (z + 200)/2
end

if a == 3 then 
x = (x - 200)/2
y = (y - 200)/2
z = (z - 200)/2
end

if a == 4 then 
x = (x + 200)/2
y = (y - 200)/2
z = (z - 200)/2
end

if a == 5 then 
x = (x + 0)/2
y = (y + 200)/2
z = (z + 0)/2
end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,y,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

Sierpinksy

Sierpinsky

This won't make a mathematical recreation of the Sierpinksy fractal, but it will merely make a pretty visual representation of it. 

x=1
y=1

for i = 50, 1, -1 do

x=i
y=(50-i)
z=(50-i)

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,i,1))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)

end


for i = 50, 1, -1 do

x=i
y=(50-i)
z=(50-i)

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+50,i,1+50))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)

end

for i = 50, 1, -1 do

x=i
y=(50-i)
z=(50-i)

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+50,i,1))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)

end

for i = 50, 1, -1 do

x=i
y=(50-i)
z=(50-i)

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,i,1+50))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)

end

for i = 50, 1, -1 do

x=i
y=(50-i)
z=(50-i)

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+25,i+50,1+25))
p.Size = Vector3.new(y,1,z)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(1)

end

Fern leaf

Fern leaf fractal
x = 1
y = 1.8
z = 1
for i = 1, 500 do
a = math.random(1,100)

if a == 1 then

x = 0
z = (0.16*z)

elseif a > 1 and a <= 8 then

x = ((0.20*x) - (0.26*z))
z= (0.23*x + 0.22*z + 16)

elseif a > 8 and a <= 15 then

x = ((-0.15*x) + 0.28*z)
z = (0.26*x + 0.24*z + 4.4)

elseif a > 15 and a <= 100 then

x = 0.85*x + 0.04*z
z = ((-0.04*x) + 0.85*z + 16)

end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
wait(.1)
end

Mandelbrot set

Mandelbrot set

This image requires the Output window of Roblox studio. Thanks to Serveringhaus.org for this code. 

iter=100
esclim=2.0
ulx=-2.0
uly=1.0
lrx=1.0
lry=-1.0
width=70
height=40

function abs(x,y)
    return math.sqrt(x*x+y*y)
end

function escapeq(cx,cy)
    local zx=0.0
    local zy=0.0
    local i=0

    while i<iter and abs(zx,zy)<esclim do
        tmp=zx*zx-zy*zy
        zy=2.0*zx*zy
        zx=tmp

        zx=zx+cx
        zy=zy+cy
        i=i+1
    end

    return i<iter
end

for y=1,height do
    line=''
    for x=1,width do
        zx=ulx+(lrx-ulx)/width*x;
        zy=uly+(lry-uly)/height*y;
        if escapeq(zx,zy) then
            line=line..'.'
        else
            line=line..'#'
        end
    end
    print(line);
end

Mandelbrot Brick Set

Brick version of the Mandelbrot Fractal

This is almost identical to the script above, but it uses bricks instead of the Output menu. 

iter=100
esclim=2.0
ulx=-2.0
uly=1.0
lrx=1.0
lry=-1.0
width=70
height=40

function abs(x,y)
    return math.sqrt(x*x+y*y)
end

function escapeq(cx,cy)
    local zx=0.0
    local zy=0.0
    local i=0

    while i<iter and abs(zx,zy)<esclim do
        tmp=zx*zx-zy*zy
        zy=2.0*zx*zy
        zx=tmp

        zx=zx+cx
        zy=zy+cy
        i=i+1
    end

    return i<iter
end

for y=1,height do
    for x=1,width do
        zx=ulx+(lrx-ulx)/width*x;
        zy=uly+(lry-uly)/height*y;
        if escapeq(zx,zy) then
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,y))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
        else
p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,y))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
--p.Color = Color3.new(2)
p.Parent = game.Workspace
--wait(.1)
        end
    end
end

Cantor set

2D Cantor set
x = 0
y = 1.8
z = 0
for i = 1, 3000 do
a = math.random(1,4)

if a == 1 then 
x = (x - 250)/3
z = (z - 250)/3
end

if a == 2 then 
x = (x - 250)/3
z = (z + 250)/3
end

if a == 3 then 
x = (x + 250)/3
z = (z + 250)/3
end

if a == 4 then 
x = (x + 250)/3
z = (z - 250)/3
end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

3D Cantor set

3D Cantor set

WARNING This can freeze up your computer. If you have a slow computer, reduce the "For" loop to a lower number, like 500, then work your way up to 1000. 

local x = 0
local y = 1.8
local z = 0

for i = 1, 2000 do
a = math.random(1,8)

if a == 1 then 
x = (x - 250)/3
y = (y - 250)/3
z = (z - 250)/3
end

if a == 2 then 
x = (x - 250)/3
y = (y - 250)/3
z = (z + 250)/3
end

if a == 3 then 
x = (x - 250)/3
y = (y + 250)/3
z = (z - 250)/3
end

if a == 4 then 
x = (x - 250)/3
y = (y + 250)/3
z = (z + 250)/3
end

if a == 5 then 
x = (x + 250)/3
y = (y + 250)/3
z = (z + 250)/3
end

if a == 6 then 
x = (x + 250)/3
y = (y - 250)/3
z = (z + 250)/3
end

if a == 7 then 
x = (x + 250)/3
y = (y + 250)/3
z = (z - 250)/3
end

if a == 8 then 
x = (x + 250)/3
y = (y - 250)/3
z = (z - 250)/3
end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,y,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

3D Cantor set 2

3D Cantor set

This is a proportional representation of the 3D Cantor set. 

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17+66,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17+66,1+66))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1+66,17+66,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,17+66,1))
p.Size = Vector3.new(33,33,33)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace

Untitled

Untitled
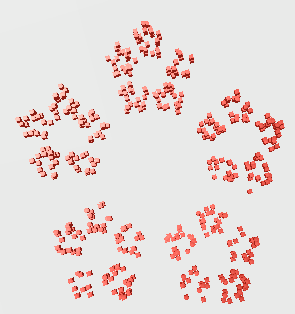
x = 68
y = 1.8
z = 56
for i = 1, 500 do
a = math.random(1,5)

if a == 1 then 
x = x / 3
z = (z - 57)/3
end

if a == 2 then 
x = (x + 68)/3
z = (z - 13)/3
end

if a == 3 then 
x = (x + 42)/3
z = (z + 58)/3
end

if a == 4 then 
x = (x - 42)/3
z = (z + 58)/3
end

if a == 5 then 
x = (x - 68)/3
z = (z - 13)/3
end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

Untitled2

Untitled
x = 82
y = 1.8
z = 30
for i = 1, 500 do
a = math.random(1,6)

if a == 1 then 
x = (x - 185)/5
z = (z - 300)/5
end

if a == 2 then 
x = (x + 180)/5
z = (z - 300)/5
end

if a == 3 then 
x = (x + 345)/5
z = (z + 5)/5
end

if a == 4 then 
x = (x + 175)/5
z = (z + 300)/5
end

if a == 5 then 
x = (x - 180)/5
z = (z + 300)/5
end

if a == 6 then 
x = (x - 350)/5
z = (z + 5)/5
end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

Quadratic Koch, 2nd iteration

Quadratic Koch, 3D (type 1), 2nd iteration

This doesn't get into the math behind it. See wikipedia for more info. 

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(1,16.2,0))
p.Size = Vector3.new(30,30,30)
p.Anchored = true
p.Color = Color3.new(0)
p.formFactor = "Symmetric"
p.Parent = game.Workspace


p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,21,0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"


p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,16.2,20))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(21,16.2,0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"


p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-19,16.2,0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"


p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,16.2,-20))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"


p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0,6.2,30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-29, 6.2, 0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(0, 6.2, -30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(31, 6.2, 0))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(31, 6.2, -30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-30, 6.2, -30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(-29, 6.2, 30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(30, 6.2, 30))
p.Size = Vector3.new(10,10,10)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
p.formFactor = "Symmetric"

Vicsek Fractal

I don't know why the middle is kicked off at an angle
x = 50
y = 1.8
z = 50
for i = 1, 1000, 1  do
a = math.random(1,5)

if a == 1 then 
x = .33*x - 66
z = .33*z + 66
end

if a == 2 then 
x = .325*x +.325*z 
z = -.325*x+.325*z
end

if a == 3 then 
x = .33*x - 66
z = .33*z - 66
end

if a == 4 then 
x = .33*x + 66
z = .33*z - 66
end

if a == 5 then 
x = .33*x + 66
z = .33*z + 66
end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

Fractal from my old calculus book

I don't know the name of this one. It's lopsided for some reason.

fractal from my old calculus book
x = 50
y = 1.8
z = 50
for i = 1, 2000, 1  do
a = math.random(1,5)

if a == 1 then 
x = (.25*x) - 25
z = .25*z + 25
end

if a == 2 then 
x = .288*x -(.167*z) - 50
z = .167*x +.288*z - 50
end

if a == 3 then 
x = (.25*x)-74.6
z = .25*z+74.6
end

if a == 4 then 
x = .5*x+50
z = .5*z-50
end

if a == 5 then 
x = .18*x+.174*z+50
z = (-.174*x)+.18*z+50
end

p = Instance.new("Part")
p.CFrame = CFrame.new(Vector3.new(x,1.8,z))
p.Size = Vector3.new(1,1,1)
p.Anchored = true
p.Color = Color3.new(1)
p.Parent = game.Workspace
--wait(.1)
end

Other Roblox Fractal images

3D Cantor dust Third iteration of 3D Koch quadratic fractal Square koch 3
Sierpinsky triangle fractal Variation of the Sierpinsky triangle fractal Vicsek fractal
Fractal T Fractal kite

See Also

Wikipedia article on Fractals

Beauty in Mathematics, an introductory article on fractals with helpful images

Retrieved from "https://rbxlegacy.wiki/index.php?title=Fractals&oldid=47700"